Dãy số Fibonacci huyền bí

Leonardo Pisano Bogollo (khoảng 1170 – khoảng 1250), còn được biết đến với tên Leonardo của Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, hay, phổ biến nhất, chỉ là Fibonacci, là một nhà toán học người Ý, được một số người xem là "nhà toán học tài ba nhất thời Trung Cổ".

Fibonacci nổi tiếng trong thế giới hiện đại vì có công lan truyền hệ ký số Hindu-Ả Rập ở châu Âu, chủ yếu thông qua việc xuất bản vào đầu thế kỷ 13 trong cuốn Sách tính toán (Liber Abaci) của ông và dãy số hiện đại mang tên ông, số Fibonacci, tuy ông không phải là người khám phá nhưng đã dùng nó làm ví dụ trong cuốn Liber Abaci.

(Dãy số này đã được các nhà toán học Ấn Độ biết đến từ thế kỷ thứ 6, nhưng chỉ đến khi cuốn Liber Abaci của Fibonacci ra đời, nó mới được giới thiệu đến phương Tây).
 

Cách thành lập dãy Số Fibonacci:

Dãy Fibonacci là dãy vô hạn các số tự nhiên bắt đầu bằng hai phần tử 0 và 1, các phần tử sau đó được thiết lập theo quy tắc mỗi phần tử luôn bằng tổng hai phần tử trước nó.

Như thế 0+1=1; 1+1=2. Số kế nữa sẽ là 3. Và số kế là 2+3=5. Kế tiếp, 3+5=8. Dưới đây là một dãy số Fibonacci:

0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, v.v…

Người ta chứng minh được rằng công thức tổng quát cho dãy Fibonacci là:

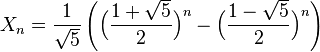
Bây giờ chắc các bạn sẽ hỏi: "Dãy số này có gì đặc biệt?"

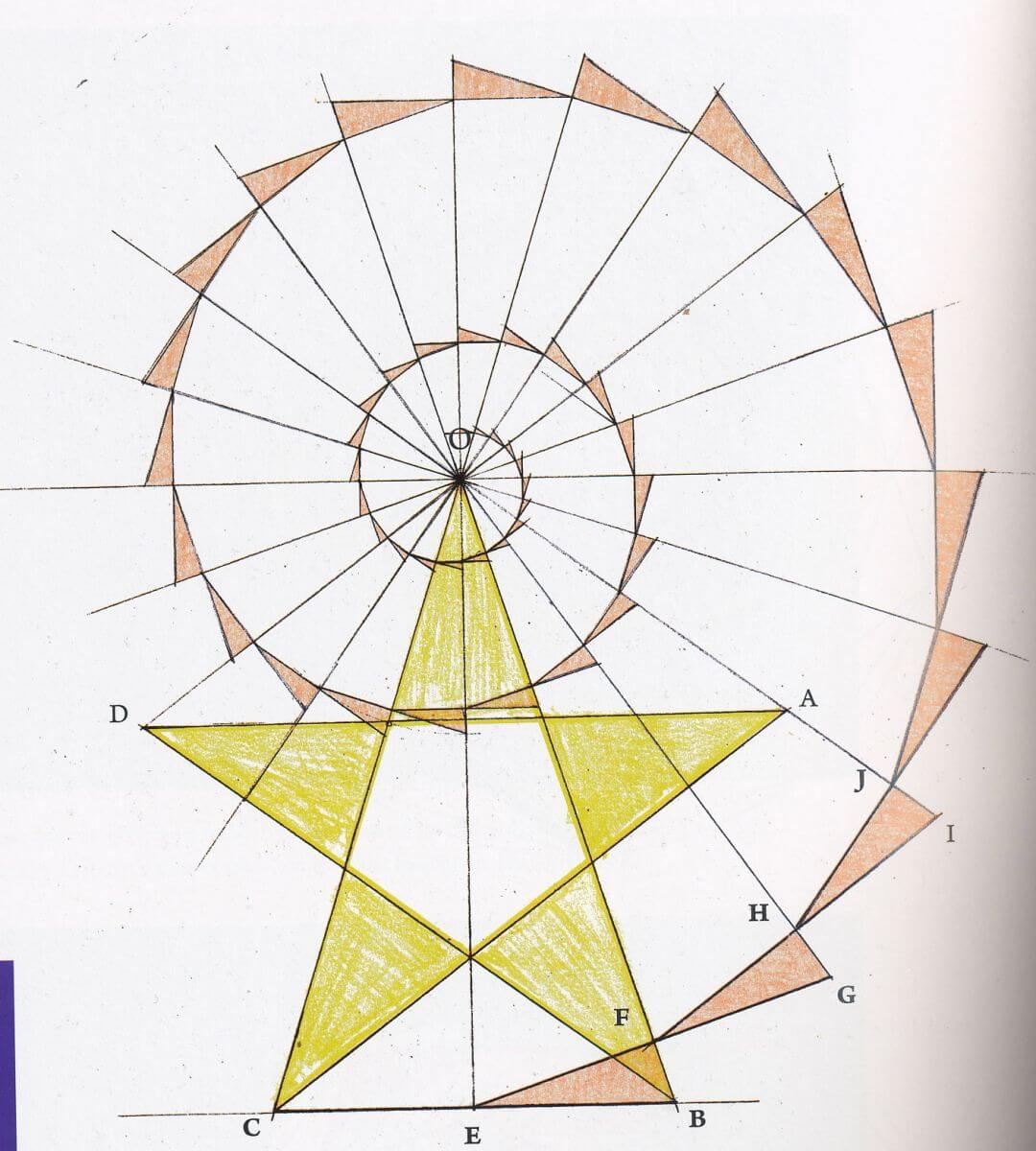
Liên quan đến tỉ lệ vàng:

Nào, mời bạn hãy xem sự tương quan về tỷ lệ giữa những con số kế nhau:

2/1 = 2.0
3/2 = 1.5
5/3 = 1.67
8/5 = 1.6
13/8 = 1.625
21/13 = 1.6153
34/21 = 1.6190
55/34 = 1.6176 
89/55 = 1.6181
144/89 = 1.6179

Bạn thấy chưa! Nếu ta tiếp tục kéo dài dãy số, tỷ lệ giữa con số hiện có - chia cho con số trước nó có vẻ hợp nhất thành một trị số là 1.618. 

Giả dụ ta tiếp tục với những con số lớn hơn, thương số của chúng càng gần nhau hơn và cuối cùng con số ấy là 1.618. Con số này chính là tỷ số vàng mà chúng ta đang tìm hiểu:

Tỷ số vàng là một số vô tỷ: nó có vô cùng tận những con số lẻ sau dấu chấm và nó không hề lập lại giống nhau. Lấy 3 số lẻ, ta có 1.618. Một trong những điểm thú vị nữa là tỷ lệ nghịch của nó: 1/1.618 = 0.618.

Lạ lùng thay một trị số và nghịch đảo của nó có những con số lẻ giống nhau. Thực ra, ta không thể tìm được một con số nào khác có đặc tính ấy. Điều gì làm chúng trở nên quá đặc biệt như thế?

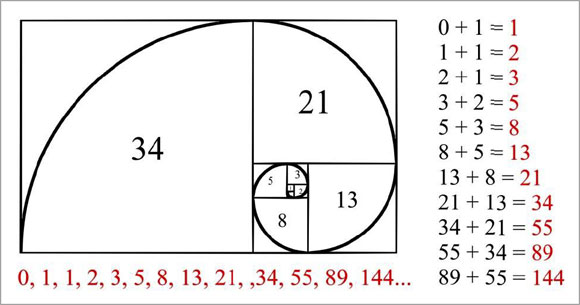
The Fibonacci spiral: an approximation of the golden spiral created by drawing circular arcs connecting the opposite corners of squares in the Fibonacci tiling; this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13, 21, and 34.

Dãy Số Fibonacci trong thiên nhiên:

Dãy Fibonacci xuất hiện ở khắp nơi trong thiên nhiên. Những chiếc lá trên một nhành cây mọc cách nhau những khoảng tương ứng với dãy số Fibonacci. Các số Fibonacci xuất hiện trong những bông hoa. Ngoài ra, số Fibonacci còn được tìm thấy trong sự sắp xếp chồi lá trên thân cây, sừng động vật, gia phả loài ong đực, dạng vòng xoáy trong quả thông, trái khóm… 

Hầu hết các bông hoa có số cánh hoa là một trong các số: 3,5,8,13,21,34,55 hoặc 89. Hoa loa kèn có 3 cánh, hoa mao lương vàng có 5 cánh, hoa phi yến thường có 8 cánh, hoa  cúc vạn thọ có 13 cánh, hoa cúc tây có 21 cánh, hoa cúc thường có 34, hoặc 55 hoặc 89 cánh.

Yellow Chamomile head showing the arrangement in 21 (blue) and 13 (aqua) spirals. Such arrangements involving consecutive Fibonacci numbers appear in a wide variety of plants.

Các số Fibonacci cũng xuất hiện trong các bông hoa hướng dương. Những nụ nhỏ sẽ kết thành hạt ở đầu bông hoa hướng dương được xếp thành hai tập các đường xoắn ốc: một tập cuộn theo chiều kim đồng hộ, còn tập kia cuộn ngược theo chiều kim đồng hồ. Số các đường xoắn ốc hướng thuận chiều kim đồng hồ thường là 34 còn ngược chiều kim đồng hồ là 55. Đôi khi các số này là 55 và 89, và thậm chí là 89 và 144. Tất cả các số này đều là các số Fibonacci kết tiếp nhau (tỷ số của chúng tiến tới tỷ số vàng).

Illustration of Vogel's model forn = 1 … 500

Trái thông cũng vậy. Vòng xoáy từ trung tâm có 5 và 8 nhánh. 

Trái khóm có 3 xoáy là 5, 8 và 13. Lại một bằng chứng những con số này không phải ngẫu nhiên. Thiên nhiên chơi trò toán học với chúng ta? Không ai biết nhưng các khoa học gia suy đoán rằng các loài thực vật mọc theo hình thể xoáy ốc theo những con số Fibonacci vì nó tiết kiệm nhiều bề mặt hơn. Sắp xếp như thế, chúng gia tăng điều kiện tăng trưởng và do đó, nhiều điều kiện sinh tồn hơn. 

Thuyết tiến hóa và dãy số Fibonacci:

So sánh thuyết tiến hóa và dãy số Fibonacci, ta thấy có điểm trùng hợp là con số hiện tại là tổng hợp 2 con số trước đó, cũng như sinh vật hiện tại thường là phối hợp những đặc điểm của những sinh vật trước đó. Nói khác đi, dãy số Fibonacci và thuyết sinh vật tiến hóa đặt nền tảng trên sự thừa kế các đặc điểm trước đó (cả ưu điểm lẫn khuyết điểm). Nó có lợi cho sự thích nghi môi trường nhưng không phải là không có hại.

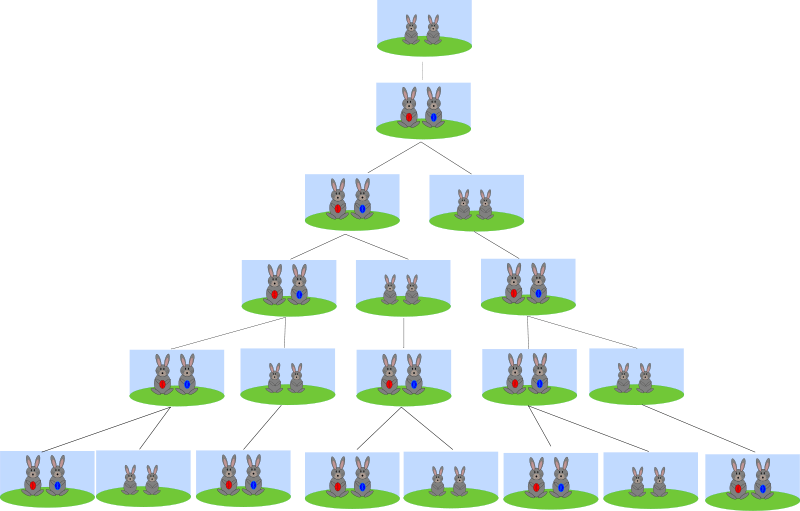
The number of rabbits form the Fibonacci sequence

Tuy nhiên, dãy số Fibonacci không phải là quy luật tất yếu về tiến hóa. Nó không giải thích được sự đứt quãng (Non-linearity), sự bất biến, sự đột biến xảy ra trong vũ trụ. Vạn vật tiến hóa theo nhiều tiến trình khác nhau. Ngoài tiến trình liên tục (linear) như Fibonacci, còn nhiều tiến trình khác như luỹ cấp (sự phân bào, 1 tế bào tự bình phương), tiến trình chu kỳ (sự vận hành quả đất, 4 mùa, động cơ máy nổ v.v...), tiến trình mạng lưới (Tàu có câu :"một cái rung cánh của con bướm ở Chợ Lớn có thể là nguồn gây hạn hán hay lụt lội ở Hoa Thịnh Đốn. Ngạn ngữ này cho thấy các biến động trong thiên nhiên đan mắc với nhau như mạng lưới), và hiện đại hơn, cơ học lượng tử cho thấy có những sự kiện tự nẩy sinh bất chấp luật nhân quả.

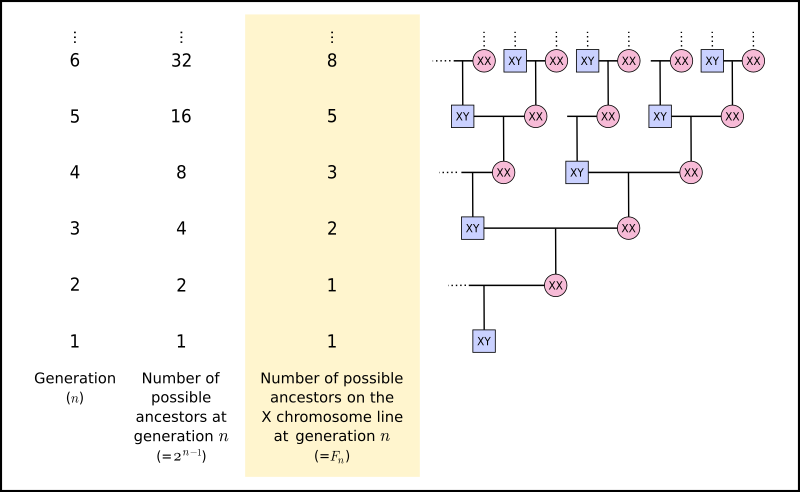
The number of possible ancestors on the X chromosome inheritance line at a given ancestral generation follows the Fibonacci sequence. (After Hutchison, L. "Growing the Family Tree: The Power of DNA in Reconstructing Family Relationships")

Fibonacci là một chuỗi số thú vị nhưng nó không tiêu biểu cho định luật thiên nhiên mà chỉ là một dạng thức ngoạn mục trong một vũ trụ đa dạng và biến đổi không ngừng.

The Fibonacci numbers are the sums of the "shallow" diagonals (shown in red) of Pascal's triangle.

Relax với chuỗi Finonacci: Một bài thơ theo bố cục chuỗi số Fibonacci:

A

Fib

can be

confusing

if you hated sums. 

Mathematics is more than that -

it can take you to a world where beauty is abstract.